-
![[image]](https://www.balancer.ru/cache/sites/ru/to/topwar/uploads/posts/2019-03/128x128-crop/1553115045_14-one-stage-termonuclear-device-with-emt.jpg)
Прецизионный одноступенчатый ядерный заряд мощностью до 1 Ктн. Новая надежда Америки?
Как работает эта странная схема ядерного заряда? Фейк или за этим что-то есть?Теги:
Полл> Часть очень нужная, но, без обид, не инфантерия совершенно.
Если под инфантерией понимать "штурмовые отряды" (элита протыкающая прорыв) - то да. А если обычное пушечное мясо (заполняющее прорыв следом) - то сойдет! Во всяком случае в военном билете написано "мотострелок". Хотя мне больше нравится вторая запись (по ней я и служил): "мастер по ремонту и обслуживанию ИТСО и телевидения, третьего класса" Но и по первой записи отсекать по два патрона меня научили на уровне рефлексов. Столько сколько мы стреляли на стрельбище никакая "пехота" не стреляла.
Но и по первой записи отсекать по два патрона меня научили на уровне рефлексов. Столько сколько мы стреляли на стрельбище никакая "пехота" не стреляла.
Полл> Ядерные заряды есть очень разные по конструкции.
Полл>. . .
Полл>Что позволит понять, как их планировалось использовать, и уже исходя из этого можно будет оценивать радиоактивное заражение.
А я об этом и говорил.
Полл> Военным не нужны "новое поколение ядерных бомб". Военным нужна система оружия, соответствующая заданным, и зачастую очень противоречивым ТТЗ.
И для этого им нужно новое ядерное оружие. Старое с самого начала их в общем то не устраивает.
Полл> Про какие системы оружия нового поколения ты говоришь?
Я же сказал. 4-го поколения. Ядерное. Маломощное (10-100-1000 т тнт не выше). "Чистое" (или совсем без продуктов деления, либо с пониженным выходом продуктов) и с управляемым выходом энергии (например повышенный или пониженный нейтронный поток, направленное действие).
Вы вообще что-нибудь СЛЫШАЛИ о таком оружии?
Если вы интересуетесь самыми передовыми идеями в этом смысле - то должны были бы.
Вот вам прямая ссылка.
Ядерное оружие четвертого поколения: Военная эффективность и побочные эффекты
Конечно на английском. Но было бы желание прочесть. Переводчики нынче очень даже неплохо переводят.
Я не думаю что вы понимаете проблему глубже, чем авторы этого исследования.
А учитывая, что я это прочел а вы вряд ли, я пока что понимаю вопрос глубже чем вы.
Так что не надо тут пыжиться (ни вам ни мне). Давайте просто обсудим интересную тему без наездов (мол у кого на погонах звезд больше!).
Полл> Позиционный тупик сегодня на оперативном и стратегических уровнях, на тактическом уровне нет никакой проблемы перекопать любую укрепленную позицию достаточно для уничтожения сопротивления.
Хотя в целом согласен (военные - молодцы, политики - бл...ди) Но мы ведь говорим о АМЕРИКАНСКИХ военных. А они как привыкли с индейцами воевать, так и норовят воевать до сих пор. Превосходя противника настолько, насколько можно. И говорить что новое оружие не нужно (даже если оно возможно) - это простите, детский лепет. Почитайте ироничный рассказ Гарри Гаррисона "Абсолютное оружие" Тут даже не в американцах дело.
Вы (как мне кажется) явно не улавливаете текущую историческую динамику. А она такова. Последние пол века (то есть вся моя жизнь и наверняка ваша) мир двигался к глобализации и это ТОРМОЗИЛО развитие многих технологий, в том числе и военных (например наш провал с выходом в космос, почему на Луне нас до сих пор нет - прямое следствие глобализации). Но процесс остановился и пошел вспять (Вавилонская башня глобализации начала рушится толком не достроенная, опять уже в третий раз в истории европейской цивилизации за последние 5 000 лет). И поэтому многие идеи, которые до сих пор тормозились как "немыслимые", "опасные", теперь "вырвутся на свободу" и побегут наверстывать упущенное. Оком не успеете моргнуть!
Если под инфантерией понимать "штурмовые отряды" (элита протыкающая прорыв) - то да. А если обычное пушечное мясо (заполняющее прорыв следом) - то сойдет! Во всяком случае в военном билете написано "мотострелок". Хотя мне больше нравится вторая запись (по ней я и служил): "мастер по ремонту и обслуживанию ИТСО и телевидения, третьего класса"
 Но и по первой записи отсекать по два патрона меня научили на уровне рефлексов. Столько сколько мы стреляли на стрельбище никакая "пехота" не стреляла.
Но и по первой записи отсекать по два патрона меня научили на уровне рефлексов. Столько сколько мы стреляли на стрельбище никакая "пехота" не стреляла.Полл> Ядерные заряды есть очень разные по конструкции.
Полл>. . .
Полл>Что позволит понять, как их планировалось использовать, и уже исходя из этого можно будет оценивать радиоактивное заражение.
А я об этом и говорил.
Полл> Военным не нужны "новое поколение ядерных бомб". Военным нужна система оружия, соответствующая заданным, и зачастую очень противоречивым ТТЗ.
И для этого им нужно новое ядерное оружие. Старое с самого начала их в общем то не устраивает.
Полл> Про какие системы оружия нового поколения ты говоришь?
Я же сказал. 4-го поколения. Ядерное. Маломощное (10-100-1000 т тнт не выше). "Чистое" (или совсем без продуктов деления, либо с пониженным выходом продуктов) и с управляемым выходом энергии (например повышенный или пониженный нейтронный поток, направленное действие).
Вы вообще что-нибудь СЛЫШАЛИ о таком оружии?
Если вы интересуетесь самыми передовыми идеями в этом смысле - то должны были бы.
Вот вам прямая ссылка.
Ядерное оружие четвертого поколения: Военная эффективность и побочные эффекты
Конечно на английском. Но было бы желание прочесть. Переводчики нынче очень даже неплохо переводят.
Я не думаю что вы понимаете проблему глубже, чем авторы этого исследования.
А учитывая, что я это прочел а вы вряд ли, я пока что понимаю вопрос глубже чем вы.
Так что не надо тут пыжиться (ни вам ни мне). Давайте просто обсудим интересную тему без наездов (мол у кого на погонах звезд больше!).
Полл> Позиционный тупик сегодня на оперативном и стратегических уровнях, на тактическом уровне нет никакой проблемы перекопать любую укрепленную позицию достаточно для уничтожения сопротивления.
Хотя в целом согласен (военные - молодцы, политики - бл...ди) Но мы ведь говорим о АМЕРИКАНСКИХ военных. А они как привыкли с индейцами воевать, так и норовят воевать до сих пор. Превосходя противника настолько, насколько можно. И говорить что новое оружие не нужно (даже если оно возможно) - это простите, детский лепет. Почитайте ироничный рассказ Гарри Гаррисона "Абсолютное оружие" Тут даже не в американцах дело.
Вы (как мне кажется) явно не улавливаете текущую историческую динамику. А она такова. Последние пол века (то есть вся моя жизнь и наверняка ваша) мир двигался к глобализации и это ТОРМОЗИЛО развитие многих технологий, в том числе и военных (например наш провал с выходом в космос, почему на Луне нас до сих пор нет - прямое следствие глобализации). Но процесс остановился и пошел вспять (Вавилонская башня глобализации начала рушится толком не достроенная, опять уже в третий раз в истории европейской цивилизации за последние 5 000 лет). И поэтому многие идеи, которые до сих пор тормозились как "немыслимые", "опасные", теперь "вырвутся на свободу" и побегут наверстывать упущенное. Оком не успеете моргнуть!

A.s.>> УПОРНО БАСНЕ
s.t.> с таким текстом вы автоматически попадаете в категорию фриков прочих ненормальных.
Может я и фрик, но я не теряю здравомыслия от избытка "образования".
Надо быть круглым идиотом чтобы верить, что распыленные 4 кг непрореагировашено заряда (уран-235, плутоний) буде давать больше заражение области, чем разделившийся во взрыве 1 кг (20 кт) актиноида!

Например наш уважаемый Виверн очень долго эту глупость тут сеял как "доброе, мудрое вечное".
И даже когда всякие там Татарины и Факиры его одергивали, он все равно продолжал это тут нести.
Со всем уважением к Виверну. Все мы - люди. И всех нас порой клинит. Для чего просто аргументов мало. Надо двать и подзатыльники (сам получал и балгадарен за это)!

Есть просто ошибки, а есть стойкие массовые заблуждения (порой специально насаженные). И УПОРОТЫЙ бред, растиражированный в неразвитых мозгах (и потому цепко защищаемый массовым носителем) надо вышибать очень крепкими пинками!
s.t.> Давайте, выкладывайте свою революсионную схему бомбы. Уверен, она у вас есть.
У меня есть только общие соображения и догадки.
Какой-то особой схемы нет.
Но выше я привел две "гипотетические" схемы. И это наводит на мысль,что у данного "дыма" должен быть и огонь. Но где? Я не знаю пока. Давайте поищем вместе.

"Революционную" схему бомбы я придумал. Но она из другой "оперы".

s.t.> с таким текстом вы автоматически попадаете в категорию фриков прочих ненормальных.
Может я и фрик, но я не теряю здравомыслия от избытка "образования".
Надо быть круглым идиотом чтобы верить, что распыленные 4 кг непрореагировашено заряда (уран-235, плутоний) буде давать больше заражение области, чем разделившийся во взрыве 1 кг (20 кт) актиноида!
Например наш уважаемый Виверн очень долго эту глупость тут сеял как "доброе, мудрое вечное".
И даже когда всякие там Татарины и Факиры его одергивали, он все равно продолжал это тут нести.
Со всем уважением к Виверну. Все мы - люди. И всех нас порой клинит. Для чего просто аргументов мало. Надо двать и подзатыльники (сам получал и балгадарен за это)!

Есть просто ошибки, а есть стойкие массовые заблуждения (порой специально насаженные). И УПОРОТЫЙ бред, растиражированный в неразвитых мозгах (и потому цепко защищаемый массовым носителем) надо вышибать очень крепкими пинками!
s.t.> Давайте, выкладывайте свою революсионную схему бомбы. Уверен, она у вас есть.
У меня есть только общие соображения и догадки.
Какой-то особой схемы нет.
Но выше я привел две "гипотетические" схемы. И это наводит на мысль,что у данного "дыма" должен быть и огонь. Но где? Я не знаю пока. Давайте поищем вместе.

"Революционную" схему бомбы я придумал. Но она из другой "оперы".


Полл>> Позиционный тупик сегодня на оперативном и стратегических уровнях, на тактическом уровне нет никакой проблемы перекопать любую укрепленную позицию достаточно для уничтожения сопротивления.
с.т.> единственное что останавливает военных от перекапывания жилой застройки - это когда им политики руки связывают, ну и гуманистические соображения. а так технически они и без ЯО отлично могут в щебёнку раскатать.
Не выдумывайте. Политики - это отмазка.
Чечня, Донбас, Сирия показывают, что каменные (а тем более бетонные хрущобы!) - для обычного оружия очень стойкое препятствие. Типичный современный город после массовой бомбежек и обстрелов быстро превращается в лабиринт-крепость, который только СНОСИТЬ ПОД ЧИСТУЮ (на что уже взрывчатки и нету) или вести длинные "сталинградские" штурмовые операции (для чего нужны очень подготовленные и мотивированные войска). То есть "пуля - дура, штык - молодец".
Кстати, для ядерного оружия обычный город из хрущоб тоже препятствие немалое. Мы просто уже более полувека живем в мире. И поэтому тешим иллюзиями что у нас есть такие большие-большие пушки (бомбы, самолеты, ракеты!!!). Нихрена это по-большому счету не стоит. Мао 1000 раз прав...
Верх глупости думать что у вас в руках - абсолютное оружие.
Оружия всегда МАЛО. Его никогда нельзя перестать совершенствовать.
с.т.> единственное что останавливает военных от перекапывания жилой застройки - это когда им политики руки связывают, ну и гуманистические соображения. а так технически они и без ЯО отлично могут в щебёнку раскатать.
Не выдумывайте. Политики - это отмазка.
Чечня, Донбас, Сирия показывают, что каменные (а тем более бетонные хрущобы!) - для обычного оружия очень стойкое препятствие. Типичный современный город после массовой бомбежек и обстрелов быстро превращается в лабиринт-крепость, который только СНОСИТЬ ПОД ЧИСТУЮ (на что уже взрывчатки и нету) или вести длинные "сталинградские" штурмовые операции (для чего нужны очень подготовленные и мотивированные войска). То есть "пуля - дура, штык - молодец".
Кстати, для ядерного оружия обычный город из хрущоб тоже препятствие немалое. Мы просто уже более полувека живем в мире. И поэтому тешим иллюзиями что у нас есть такие большие-большие пушки (бомбы, самолеты, ракеты!!!). Нихрена это по-большому счету не стоит. Мао 1000 раз прав...
Атомная бомба — это бумажный тигр, которым американские реакционеры запугивают людей, с виду он кажется страшным, а на самом деле вовсе не страшен. Конечно, атомная бомба — это оружие массового истребления, однако исход войны решает народ, а не один-два новых вида оружия.
Мао Цзэдун. Беседа с американской журналисткой Анной Луизой Стронг (6 августа 1946 г.)
Верх глупости думать что у вас в руках - абсолютное оружие.
Оружия всегда МАЛО. Его никогда нельзя перестать совершенствовать.

A.s.> Но выше я привел две "гипотетические" схемы. И это наводит на мысль,что у данного "дыма" должен быть и огонь. Но где? Я не знаю пока. Давайте поищем вместе.
Т.е Вы предлагаете на Авиабазе разработать Новую , Революционную схему . Ну , или , по крайней мере , обсудить Ваши Гипотезы? Зачем? Задумываетесь , как воплотить в жись? Подсказать Зеленскому? Нее ..Народ здесь ушлый , после того , как заблокировали А-базу из-за фиговинки , в старых постах по какой-то штукенции .. (А вдруг и Иран читает Форум? И , не дай бог , КНДР)...Всю Россию вгоните в "санкции"...
(А вдруг и Иран читает Форум? И , не дай бог , КНДР)...Всю Россию вгоните в "санкции"...
PS А вообще - есть же стандартная , простейшая Схема . 4 Кг стали для обжатия + 4 кг Плутония .Две Сферы , диаметром 10 см. Внутри 10 литров Дейтерия+Тритий, под давлением 10 атмосфер . При Имплозии всё сжимается в сферу в 4 см , полость с D+T в 0.4 см . И Поехали!
Т.е Вы предлагаете на Авиабазе разработать Новую , Революционную схему . Ну , или , по крайней мере , обсудить Ваши Гипотезы? Зачем? Задумываетесь , как воплотить в жись? Подсказать Зеленскому? Нее ..Народ здесь ушлый , после того , как заблокировали А-базу из-за фиговинки , в старых постах по какой-то штукенции ..
 (А вдруг и Иран читает Форум? И , не дай бог , КНДР)...Всю Россию вгоните в "санкции"...
(А вдруг и Иран читает Форум? И , не дай бог , КНДР)...Всю Россию вгоните в "санкции"...PS А вообще - есть же стандартная , простейшая Схема . 4 Кг стали для обжатия + 4 кг Плутония .Две Сферы , диаметром 10 см. Внутри 10 литров Дейтерия+Тритий, под давлением 10 атмосфер . При Имплозии всё сжимается в сферу в 4 см , полость с D+T в 0.4 см . И Поехали!


Это сообщение редактировалось 08.10.2019 в 19:31
O.N.> Т.е Вы предлагаете на Авиабазе разработать Новую , Революционную схему .
Нам не хватит ума это придумать.
O.N.>Ну , или , по крайней мере , обсудить Ваши Гипотезы? Зачем?
Для прикола!
O.N.>Задумываетесь , как воплотить в жись? Подсказать Зеленскому? Нее ..
Господи, этот то тут причем? Для Украины (не говоря уже о Зеленском) ЯО 4-го поколения это еще "круче" чем гиперлуп или база на Луне!!!
O.N.> Народ здесь ушлый , после того , как заблокировали А-базу из-за фиговинки , в старых постах по какой-то штукенции .. (А вдруг и Иран читает Форум? И , не дай бог , КНДР)...Всю Россию вгоните в "санкции"...
(А вдруг и Иран читает Форум? И , не дай бог , КНДР)...Всю Россию вгоните в "санкции"...
Гм... не слылшал о таком. А поподробней можно?
Я очень сильно сомневаюсь. Думаю это местные "городский байки".
Дело в том что это просто глупо. Лучшая стратегия в случае, если кто-то публично "придумал" секретную ядерную технологию - промолчать, сделать вид что это - обычный рядовой бред. Не подавать виду. Как говорится "без комментариев". Если же начать что-то закрывать - привлекать внимание и по-сути выболтать секрет.
O.N.> PS А вообще - есть же стандартная , простейшая Схема . 4 Кг стали для обжатия + 4 кг Плутония .Две Сферы , диаметром 10 см. Внутри 10 литров Дейтерия+Тритий, под давлением 10 атмосфер . При Имплозии всё сжимается в сферу в 4 см , полость с D+T в 0.4 см . И Поехали!
Детский сад!
Я что? В подвале бомбу делаю?
Мне не интересна ПРАКТИКА в "кружке умелые ручки". Абсолютно. Мне интересна теория оружия (притом безобидная теория, не лезущая в коды моделирования гидродинамики взрывных процессов). И вообще мне интересна следующая гипотеза: человечество в 1960-х отказалось от целой ветви технологий (ядерные взрывные) почему до сих пор и не решило ни энергетические проблемы цивилизации ни проблему выхода в космос из колыбели. При этом я виню не только естественный страх перед прогрессом (слишком быстрым он был в середине XX века) но и идеологию глобализации (коим ядерное оружие нужно было только как страшилка-жупел, миф, голова медузы Горгоны), которая (идеология) умирает у нас на глазах.
То есть мне интересны только "хформулы", графики, чертежи. Не более.
Все в безобидном первоначально-идейном виде без углубления в детали, которые позволят создать на практике такое оружие.
При этом старые добрые "бомбы" мне не интересны. Они ясны и прозрачны.
Мне интересны специальные изделия предельных возможностей (и не столько для убийства, сколько в народно-хозяйственных или космичеси-исследовательских целях. Одно не отделимо от другого. Нет мирных нет военных технологий. Любая технология - двуликий янус).
Нам не хватит ума это придумать.
O.N.>Ну , или , по крайней мере , обсудить Ваши Гипотезы? Зачем?
Для прикола!

O.N.>Задумываетесь , как воплотить в жись? Подсказать Зеленскому? Нее ..
Господи, этот то тут причем? Для Украины (не говоря уже о Зеленском) ЯО 4-го поколения это еще "круче" чем гиперлуп или база на Луне!!!
O.N.> Народ здесь ушлый , после того , как заблокировали А-базу из-за фиговинки , в старых постах по какой-то штукенции ..
 (А вдруг и Иран читает Форум? И , не дай бог , КНДР)...Всю Россию вгоните в "санкции"...
(А вдруг и Иран читает Форум? И , не дай бог , КНДР)...Всю Россию вгоните в "санкции"...Гм... не слылшал о таком. А поподробней можно?
Я очень сильно сомневаюсь. Думаю это местные "городский байки".
Дело в том что это просто глупо. Лучшая стратегия в случае, если кто-то публично "придумал" секретную ядерную технологию - промолчать, сделать вид что это - обычный рядовой бред. Не подавать виду. Как говорится "без комментариев". Если же начать что-то закрывать - привлекать внимание и по-сути выболтать секрет.
O.N.> PS А вообще - есть же стандартная , простейшая Схема . 4 Кг стали для обжатия + 4 кг Плутония .Две Сферы , диаметром 10 см. Внутри 10 литров Дейтерия+Тритий, под давлением 10 атмосфер . При Имплозии всё сжимается в сферу в 4 см , полость с D+T в 0.4 см . И Поехали!
Детский сад!
Я что? В подвале бомбу делаю?
Мне не интересна ПРАКТИКА в "кружке умелые ручки". Абсолютно. Мне интересна теория оружия (притом безобидная теория, не лезущая в коды моделирования гидродинамики взрывных процессов). И вообще мне интересна следующая гипотеза: человечество в 1960-х отказалось от целой ветви технологий (ядерные взрывные) почему до сих пор и не решило ни энергетические проблемы цивилизации ни проблему выхода в космос из колыбели. При этом я виню не только естественный страх перед прогрессом (слишком быстрым он был в середине XX века) но и идеологию глобализации (коим ядерное оружие нужно было только как страшилка-жупел, миф, голова медузы Горгоны), которая (идеология) умирает у нас на глазах.
То есть мне интересны только "хформулы", графики, чертежи. Не более.
Все в безобидном первоначально-идейном виде без углубления в детали, которые позволят создать на практике такое оружие.
При этом старые добрые "бомбы" мне не интересны. Они ясны и прозрачны.
Мне интересны специальные изделия предельных возможностей (и не столько для убийства, сколько в народно-хозяйственных или космичеси-исследовательских целях. Одно не отделимо от другого. Нет мирных нет военных технологий. Любая технология - двуликий янус).

A.s.> Гм... не слылшал о таком. А поподробней можно?
A.s.> Я очень сильно сомневаюсь. Думаю это местные "городский байки".
Смешной Вы . Тут Народ жужжал пару месяцев про блокировку , а Вы и не знаете . Только недавно Запрос был отозван.

Но из-за вас Форум может быть спокойным .Не заблокируют.
A.s.> ... человечество в 1960-х отказалось от целой ветви технологий (ядерные взрывные) почему до сих пор и не решило ни энергетические проблемы цивилизации ...
Как это не решили? Зелёные уже всё расписали , как нужно . Грета Тунберг не даст соврать .
A.s.> Я очень сильно сомневаюсь. Думаю это местные "городский байки".
Смешной Вы . Тут Народ жужжал пару месяцев про блокировку , а Вы и не знаете . Только недавно Запрос был отозван.

Авиабаза может быть недоступна
~~~На сервере проблемы с железом. balancer.ru / airbase.ru могут закрыться в любой момент на неопределённый срок. Сидим сейчас на временном сервере провайдера. Подробности и новости - на http://bal.livejournal.com [b]Update[/b]: * [http://balancer.ru/2009/09/07/p ost-2040931.html|Обобщение информации о способах переводов от Mishka] * [http://balancer.ru/2009/09/08/p ost-2042103.html|Уточнение про ИНН Альфа-банка и атрибуты перевода]// Новости АвиабазыНо из-за вас Форум может быть спокойным .Не заблокируют.
A.s.> ... человечество в 1960-х отказалось от целой ветви технологий (ядерные взрывные) почему до сих пор и не решило ни энергетические проблемы цивилизации ...
Как это не решили? Зелёные уже всё расписали , как нужно . Грета Тунберг не даст соврать .


Это сообщение редактировалось 08.10.2019 в 20:24
с.т.>> а так технически они и без ЯО отлично могут в щебёнку раскатать.
s.t.> ЯО все же дешевле.
ЯО дешевле в логистике, но дороже во всех остальных аспектах.
ИМХО по принципу "трёх П": ЯО станет дешевле обычного оружия при применении на уровне миллионов тонн тротилового эквивалента в год.
То есть на порядок больше, чем сейчас.
s.t.> ЯО все же дешевле.
ЯО дешевле в логистике, но дороже во всех остальных аспектах.
ИМХО по принципу "трёх П": ЯО станет дешевле обычного оружия при применении на уровне миллионов тонн тротилового эквивалента в год.
То есть на порядок больше, чем сейчас.


A.s.> Я же сказал. 4-го поколения. Ядерное. Маломощное (10-100-1000 т тнт не выше). "Чистое" (или совсем без продуктов деления, либо с пониженным выходом продуктов) и с управляемым выходом энергии (например повышенный или пониженный нейтронный поток, направленное действие).
A.s.> Вы вообще что-нибудь СЛЫШАЛИ о таком оружии?
Слышал. Даже читал в интернете, что в США был принят закон ЗАПРЕЩАВШИЙ разработку и принятие на вооружение ядерных устройств мощностью ниже пяти килотонн.
Принят был вроде как после карибского кризиса, то есть во второй половине двадцатого века. По-видимому после его принятия были уничтожены все американские ядерные артиллерийские снаряды.
A.s.> Вы вообще что-нибудь СЛЫШАЛИ о таком оружии?
Слышал. Даже читал в интернете, что в США был принят закон ЗАПРЕЩАВШИЙ разработку и принятие на вооружение ядерных устройств мощностью ниже пяти килотонн.
Принят был вроде как после карибского кризиса, то есть во второй половине двадцатого века. По-видимому после его принятия были уничтожены все американские ядерные артиллерийские снаряды.


haleev> Слышал. Даже читал в интернете, что в США был принят закон ЗАПРЕЩАВШИЙ разработку и принятие на вооружение ядерных устройств мощностью ниже пяти килотонн.
Ну да ... Сейчас W-76-2 , с января 2019 .
PS Вот только СПРН пофигу , какой там заряд. Пуск БРПЛ - Всё !
Ну да ... Сейчас W-76-2 , с января 2019 .
PS Вот только СПРН пофигу , какой там заряд. Пуск БРПЛ - Всё !


Это сообщение редактировалось 08.10.2019 в 20:51
A.s.> Если под инфантерией понимать "штурмовые отряды" (элита протыкающая прорыв) - то да. А если обычное пушечное мясо (заполняющее прорыв следом) - то сойдет! Во всяком случае в военном билете написано "мотострелок". Хотя мне больше нравится вторая запись (по ней я и служил): "мастер по ремонту и обслуживанию ИТСО и телевидения, третьего класса"  Но и по первой записи отсекать по два патрона меня научили на уровне рефлексов. Столько сколько мы стреляли на стрельбище никакая "пехота" не стреляла.
Но и по первой записи отсекать по два патрона меня научили на уровне рефлексов. Столько сколько мы стреляли на стрельбище никакая "пехота" не стреляла.
Я извиняюсь за офф-топ, и готов вынести его из твоей темы, если хочешь:
Инфантерии - это те, кто останавливает прорывы врага.
Те, кто знает, что от стрелковки сегодня в бою гибнет менее 10% убитых.
Те, что умеют рассаживаться взводом, ротой, батальоном по выделенному транспорту - грузовикам, джипам и пикапам, бтрам и БМП, танкам. При этом находя место для погрузки всех своих запасов. И делая это быстро.
Те, кто умеют ехать на броне сутками, ведя наблюдение и охранение конвоя. И после езды на металле под дождём или снегом, или жаре - вступать в бой сходу.
Те, что смогут по звуку стрельбы определять направление стрельбы пулемёта в километре от себя.
Те, что способны сделать из подручных материалов укрытие для себя и техники, правильно разместить на местности и замаскировать.
Те, что умеют закапываться быстро, там где надо и правильно.
Те, кто умеют наводить артиллерию и авиацию, ставить и снимать инженерные заграждения.
Те, что умеют готовить съедобную еду из того, что есть.
Те, что умеют поддерживать санитарию и лечить себя и товарищей посреди войны.
Вот это, вкратце, пехота.
А стрелять хорошо спортсмены умеют.
 Но и по первой записи отсекать по два патрона меня научили на уровне рефлексов. Столько сколько мы стреляли на стрельбище никакая "пехота" не стреляла.
Но и по первой записи отсекать по два патрона меня научили на уровне рефлексов. Столько сколько мы стреляли на стрельбище никакая "пехота" не стреляла.Я извиняюсь за офф-топ, и готов вынести его из твоей темы, если хочешь:
Инфантерии - это те, кто останавливает прорывы врага.
Те, кто знает, что от стрелковки сегодня в бою гибнет менее 10% убитых.
Те, что умеют рассаживаться взводом, ротой, батальоном по выделенному транспорту - грузовикам, джипам и пикапам, бтрам и БМП, танкам. При этом находя место для погрузки всех своих запасов. И делая это быстро.
Те, кто умеют ехать на броне сутками, ведя наблюдение и охранение конвоя. И после езды на металле под дождём или снегом, или жаре - вступать в бой сходу.
Те, что смогут по звуку стрельбы определять направление стрельбы пулемёта в километре от себя.
Те, что способны сделать из подручных материалов укрытие для себя и техники, правильно разместить на местности и замаскировать.
Те, что умеют закапываться быстро, там где надо и правильно.
Те, кто умеют наводить артиллерию и авиацию, ставить и снимать инженерные заграждения.
Те, что умеют готовить съедобную еду из того, что есть.
Те, что умеют поддерживать санитарию и лечить себя и товарищей посреди войны.
Вот это, вкратце, пехота.
А стрелять хорошо спортсмены умеют.


O.N.> Ну да ... Сейчас W-76-2 , с января 2019 .
O.N.> PS Вот только СПРН пофигу , какой там заряд. Пуск БРПЛ - Всё !
Ну да, о чём и речь. Обычная арта действует здесь и сейчас, прикрывает свои войска, участвует в артиллерийских дуэлях и не может начать ядерную войну. И полномочиями на применение этого оружия обладает, например, полковник (поправьте меня знающие люди - как соотносятся тут калибры и звания).
А маленькая ядерная боеголовка пахнет как большая.
И вопрос перемалывания в щебень этим оружием сейчас решают генштаб и главнокомандующий.
И это кмк правильно.
O.N.> PS Вот только СПРН пофигу , какой там заряд. Пуск БРПЛ - Всё !
Ну да, о чём и речь. Обычная арта действует здесь и сейчас, прикрывает свои войска, участвует в артиллерийских дуэлях и не может начать ядерную войну. И полномочиями на применение этого оружия обладает, например, полковник (поправьте меня знающие люди - как соотносятся тут калибры и звания).
А маленькая ядерная боеголовка пахнет как большая.
И вопрос перемалывания в щебень этим оружием сейчас решают генштаб и главнокомандующий.
И это кмк правильно.


Это сообщение редактировалось 08.10.2019 в 22:01
A.s.> Наиболее удивительное я выделил красным.
A.s.> Под действием сходящейся волны давления
Пусть в волне будет 30% от химэнергии. Я буду оптимистичные цифирьки брать.
A.s.> иодид цезия вырабатывает сверхмощный электромагнитный импульс,
Ну, пусть из энергии волны тоже 30% в импульс.
A.s.> поток электронов генерирует в плутонии гамма-излучение,
Тут я что-то не понял, с хера ли?
Как в рентгеновской трубке?
С КПД = 1% ?
Ну хрен с ним, пусть будет 3%.
A.s.> выбивающее нейтроны из ядер
Ну, наверное, надо будет не меньше МэВа на нейтрон.
A.s.> инициируя тем самым самораспространяющуюся реакцию деления
С хера ли "самораспространяющуюся"?
Там 10 кил плутония? Нет?
Тогда один нейтрон — 200 МэВ выделения энергии.
Итого:
0.3 * 0.3 * 0.03 * 200 = 0.54
В очень потолочно-оптимистичном случае выделение энергии деления будет меньше, чем химэнергия взрывчатки.
Чего-то горячего, чтоб "рентгеновское излучение сжимает и нагревает дейтерид лития", там не будет.
Да и в настоящих бомбах лидочку сжимают серией слабых ударных волн и тщательно стараются ничем не нагревать, чтоб сжалась как следует.
А только потом поджигают.
A.s.> Что за чудо-процесс?
Чюдо-Юдо поганое!!!
Я пытался придумать конструкцию с взрывным электрогенератором, чтоб потом током сжимать капсулу.
Там бы КПД был бы побольше. И нежнее.
Но нихрена хорошего не получилось.
Но зато посчитал активацию грунта нейтронами для 0.5 кт совершенно чистого взрыва лидочки с чистым Li6.
Чтоб не было лишних нейтронов от Li7.
Если совсем не экранировать, около 1% активации от энергии взрыва.
Получилось всё равно шибко грязно, особенно в первое время.
В первые 15 минут светит радиацией алюминий с мощностью от 20 мегаватт, спадая до 3. То есть, ночью облако пыли будет освещать всё вокруг.
Потом марганец. И ему будут помогать калий и натрий.
Через час 1 мегаватт, через сутки 40 киловатт.
Потом калий и натрий, а через неделю железо, всего 60 ватт.
И года через три останется кобальт, 0.3 ватта.
A.s.> Под действием сходящейся волны давления
Пусть в волне будет 30% от химэнергии. Я буду оптимистичные цифирьки брать.
A.s.> иодид цезия вырабатывает сверхмощный электромагнитный импульс,
Ну, пусть из энергии волны тоже 30% в импульс.
A.s.> поток электронов генерирует в плутонии гамма-излучение,
Тут я что-то не понял, с хера ли?
Как в рентгеновской трубке?
С КПД = 1% ?
Ну хрен с ним, пусть будет 3%.
A.s.> выбивающее нейтроны из ядер
Ну, наверное, надо будет не меньше МэВа на нейтрон.
A.s.> инициируя тем самым самораспространяющуюся реакцию деления
С хера ли "самораспространяющуюся"?
Там 10 кил плутония? Нет?
Тогда один нейтрон — 200 МэВ выделения энергии.
Итого:
0.3 * 0.3 * 0.03 * 200 = 0.54
В очень потолочно-оптимистичном случае выделение энергии деления будет меньше, чем химэнергия взрывчатки.
Чего-то горячего, чтоб "рентгеновское излучение сжимает и нагревает дейтерид лития", там не будет.
Да и в настоящих бомбах лидочку сжимают серией слабых ударных волн и тщательно стараются ничем не нагревать, чтоб сжалась как следует.
А только потом поджигают.
A.s.> Что за чудо-процесс?
Чюдо-Юдо поганое!!!

Я пытался придумать конструкцию с взрывным электрогенератором, чтоб потом током сжимать капсулу.
Там бы КПД был бы побольше. И нежнее.
Но нихрена хорошего не получилось.

Но зато посчитал активацию грунта нейтронами для 0.5 кт совершенно чистого взрыва лидочки с чистым Li6.
Чтоб не было лишних нейтронов от Li7.
Если совсем не экранировать, около 1% активации от энергии взрыва.
Получилось всё равно шибко грязно, особенно в первое время.
В первые 15 минут светит радиацией алюминий с мощностью от 20 мегаватт, спадая до 3. То есть, ночью облако пыли будет освещать всё вокруг.

Потом марганец. И ему будут помогать калий и натрий.
Через час 1 мегаватт, через сутки 40 киловатт.
Потом калий и натрий, а через неделю железо, всего 60 ватт.
И года через три останется кобальт, 0.3 ватта.

Xan> В первые 15 минут светит ...
А можно всё это визуально расписать ? Именно по Цветам . Шибко уж Красиво должно получиться . Пиротехникам в помощь ...
А можно всё это визуально расписать ? Именно по Цветам . Шибко уж Красиво должно получиться . Пиротехникам в помощь ...



O.N.>> А можно всё это визуально расписать ? Именно по Цветам . Шибко уж Красиво должно получиться . Пиротехникам в помощь ... 
Naib> Визуально - ярко-голубой, с нежным ультрафиолетовым оттенком.
Да!
От каких-то изотопов летит гамма, которая вышибает электроны.
От других сразу летят электроны (бета).
Все они ионизируют воздух, который при рекомбинации светит видимым (и невидимым) светом.
Как в тлеющем разряде.
Независимо от изотопа.
Но не голубой, а, скорее, розоватый. Голубым он кажется по сравнению с ночным освещением лампами накаливания или другими источниками с низкой цветовой температурой.
А днём молнии немного розоватые, если приглядеться.

Naib> Визуально - ярко-голубой, с нежным ультрафиолетовым оттенком.
Да!

От каких-то изотопов летит гамма, которая вышибает электроны.
От других сразу летят электроны (бета).
Все они ионизируют воздух, который при рекомбинации светит видимым (и невидимым) светом.
Как в тлеющем разряде.
Независимо от изотопа.
Но не голубой, а, скорее, розоватый. Голубым он кажется по сравнению с ночным освещением лампами накаливания или другими источниками с низкой цветовой температурой.
А днём молнии немного розоватые, если приглядеться.

Xan> Но не голубой, а, скорее, розоватый. Голубым он кажется по сравнению с ночным освещением лампами накаливания или другими источниками с низкой цветовой температурой.
Xan> А днём молнии немного розоватые, если приглядеться.
А черенковское излучение?
Мне кажется, что основной вклад в светимость оно должно давать.
Xan> А днём молнии немного розоватые, если приглядеться.
А черенковское излучение?
Мне кажется, что основной вклад в светимость оно должно давать.


Naib> А черенковское излучение?
Naib> Мне кажется, что основной вклад в светимость оно должно давать.
МэВные электроны летят медленнее, чем скорость света в воздухе.
В воде черенок будет, да.
ЗЫ
Склероз уже!
Это, оказывается, я считал активацию не дли лидочки, а для чистого дейтерия.
Для немножко заглублённого взрыва.
Но особой разницы не будет — другие факторы, типа борного экрана, и состав конкретного грунта гораздо сильнее влияют.
Naib> Мне кажется, что основной вклад в светимость оно должно давать.
МэВные электроны летят медленнее, чем скорость света в воздухе.
В воде черенок будет, да.
ЗЫ
Склероз уже!

Это, оказывается, я считал активацию не дли лидочки, а для чистого дейтерия.
Для немножко заглублённого взрыва.
Но особой разницы не будет — другие факторы, типа борного экрана, и состав конкретного грунта гораздо сильнее влияют.

A.s.> Ядерное. Маломощное (10-100-1000 т тнт не выше).
Зачем? Для какого рода конфликта и поражения каких целей?
(Полл выше написал - как оно решается в реале, просто и недорого.)
A.s.> ...Но мы ведь говорим о АМЕРИКАНСКИХ военных...
Судя по всему - они требуют УМЕНЬШЕНИЯ калибра и повышения ТОЧНОСТИ, как легко видеть на примере SDB. Там где нужны большие бомбы - появились МОАП и МОАБ (как раз 10т, за недорого, для "индейцев").
A.s.> ... А они как привыкли с индейцами воевать...
Для "индейцев" ЯО - жутко избыточное средство, в том числе по цене.
A.s.> ...и это ТОРМОЗИЛО развитие многих технологий...
А многих других, в том числе военных, заметно ускорило.
A.s.> ...например наш провал с выходом в космос...
Как и наш провал в сельском хозяйстве, лёгкой промышленности, машиностроении и развитии технологий в целом - обусловлен, исключитель и только, недостатками нашей общественно-политической системы.
Зачем? Для какого рода конфликта и поражения каких целей?
(Полл выше написал - как оно решается в реале, просто и недорого.)
A.s.> ...Но мы ведь говорим о АМЕРИКАНСКИХ военных...
Судя по всему - они требуют УМЕНЬШЕНИЯ калибра и повышения ТОЧНОСТИ, как легко видеть на примере SDB. Там где нужны большие бомбы - появились МОАП и МОАБ (как раз 10т, за недорого, для "индейцев").
A.s.> ... А они как привыкли с индейцами воевать...
Для "индейцев" ЯО - жутко избыточное средство, в том числе по цене.
A.s.> ...и это ТОРМОЗИЛО развитие многих технологий...
А многих других, в том числе военных, заметно ускорило.
A.s.> ...например наш провал с выходом в космос...
Как и наш провал в сельском хозяйстве, лёгкой промышленности, машиностроении и развитии технологий в целом - обусловлен, исключитель и только, недостатками нашей общественно-политической системы.


A.s.>> ...например наш провал с выходом в космос...
hsm> Как и наш провал в сельском хозяйстве, лёгкой промышленности, машиностроении и развитии технологий в целом - обусловлен, исключитель и только, недостатками нашей общественно-политической системы.
Я смотрю вы очень целостный.... То есть у вас НА ЗАВИСТЬ монолитное моиропонимание...
Простое, общепринятое и ... Вы - счастливый человек, я думаю!
Ну да бог с вами.
Суть
Когда я говоря "мы" я имел в виду ВСЮ земную цивилизацию.
Уловили?
По поводу вашей хоровой песни "есть у нас ракеты, есть и корабли, наши космонавты- чудо всей земли!"
Послушайте. И во веки веков и во все времена были такие вот как вы "певуны". С целостным миропониманием. Мол, новое оружие УЖЕ - не нужно. У нас уже все есть!
И порох в военном деле не сходу стали применять. Было много неразумных и РАЗУМНЫХ аргументов против (действительно чудовищно расточительный способ воевать по сравнению с мечами, копьями и стрелами).
Но собака лает, а караван идет.
Лично мое мнение. Останавливать прогресс, что перегораживать реку. Накопится и прорвет. Особенно на пике НТР (а мы - на пике). Но с ядерными технологиями (и в первую очередь с взрывными) как раз нечто подобное последние пол века и делали. Ясно почему. И теперь когда мир меняется (те кто делали - идут в сад), вы глазом не успеете моргнуть, как все в КОРНЕ изменится... Ну разве что будете имитировать память аквариумной рыбки (большинство так и делают)?
hsm> Как и наш провал в сельском хозяйстве, лёгкой промышленности, машиностроении и развитии технологий в целом - обусловлен, исключитель и только, недостатками нашей общественно-политической системы.
Я смотрю вы очень целостный.... То есть у вас НА ЗАВИСТЬ монолитное моиропонимание...
Простое, общепринятое и ... Вы - счастливый человек, я думаю!
Ну да бог с вами.
Суть
Когда я говоря "мы" я имел в виду ВСЮ земную цивилизацию.
Уловили?

По поводу вашей хоровой песни "есть у нас ракеты, есть и корабли, наши космонавты- чудо всей земли!"
Послушайте. И во веки веков и во все времена были такие вот как вы "певуны". С целостным миропониманием. Мол, новое оружие УЖЕ - не нужно. У нас уже все есть!
И порох в военном деле не сходу стали применять. Было много неразумных и РАЗУМНЫХ аргументов против (действительно чудовищно расточительный способ воевать по сравнению с мечами, копьями и стрелами).
Но собака лает, а караван идет.
Лично мое мнение. Останавливать прогресс, что перегораживать реку. Накопится и прорвет. Особенно на пике НТР (а мы - на пике). Но с ядерными технологиями (и в первую очередь с взрывными) как раз нечто подобное последние пол века и делали. Ясно почему. И теперь когда мир меняется (те кто делали - идут в сад), вы глазом не успеете моргнуть, как все в КОРНЕ изменится... Ну разве что будете имитировать память аквариумной рыбки (большинство так и делают)?

По существу.
Я могу насчитать минимум ТРИ идеи как сделать мини-ядерную бомбу.
Самая простая и древняя идея - гидридная бомба (о ней я тут однажды уже спорил).
Я нашел в англоязычном интернете статью, авторы которой думают так же.
Статья спорная. Поэтому я ее перевел не всю а только начало.

первая публикация - 4 сентября 2015
Ян Гринхалх совместно Джеффом Смитом.
Сейчас мы находимся на стадии разработки пятого поколения ядерного оружия, что означает, что существует целый ряд различных типов ядерного оружия, и они существенно отличаются по эффективности от того оружия, с которым мы знакомы по всем этим киножурналам 1950-х годов об огромных атомных взрывах.
* * *
Современное ядерное оружие 5-го поколения часто имеет гораздо меньшую мощность, чем бомбы Хиросимы и Нагасаки, с выходом менее 1 килотонны (1000 тонн в тротиловом эквиваленте). У него также иная динамика взрыва - вместо одного мощного короткого взрыва у его может быть намного более длительное время горения, что производит визуальные эффекты, которые выглядят совсем по-другому.
Вот почему важно кое-что узнать об этих новых типах оружия и о том, как его взрывы будут выглядеть визуально, поскольку это позволит лучше идентифицировать ядерные инциденты в будущем; позволяя людям различать обычные взрыв на складе, битком набатом ракетным топлива от настоящего ядерного взрыва.
Микроядерный тест на маленьком трейлере, показывающий, насколько маломощными могут быть это 5-е поколение.
Не надо самих себя обманывать, мы вступили в опасную новую эпоху, когда использование этого нового передового ядерного оружия малой мощности станет все более распространенным явлением; поэтому нам всем необходимо больше информации об этом оружии, чтобы все труднее можно было скрытно использовать его для совершения террора.
* * *
Уран-гидридная бомба представляет собой вариант конструкции атомной бомбы, впервые предложенный еще в 1939 году. В ней используется дейтерий, изотоп водорода, в качестве замедлителя нейтронов в имплозивном оружии на основе U235. Здесь нейтронная цепная реакция представляет собой замедленный процесс ядерного деления по сравнению с процессом ядерного деления быстрыми нейтронами в обычном заряде.
Из-за использования более медленно движущихся нейтронов в цепном процессе, на итоговый выход взрывной мощности бомб охлаждение нейтронов оказывает отрицательно влияет, поскольку оно растягивает во времени процесс размножения нейтронов или снижает скорость производства альфа. Достоверно известно, что две уран-гидридные бомбы были испытаны еще в 1950-х годах, при испытательных взрывах Рут и Рэй (Ruth and Ray) в ходе операции Upshot-Knothole, в 1956 году. Испытания выдали мощность, сравнимую примерно с 200 тоннами тротила каждое. Тем не менее, в то время оба теста считались неэффективными. Так как тогда была тенденция создавать оружия с большим взрывом выходом и технология была отложена на более чем 20 лет.
В конструкции такого ядерного оружия на замедленном или медленном делении, дейтерий в форме гидрида урана (UH3) или гидрида плутония (PUH3) замедляет (притормаживает) нейтроны, тем самым увеличивая сечение деления нейтронов. В результате достигается гораздо меньшая критическая масса и, следовательно, более компактное оружие, в котором снижается количество U235 или плутония PU239, необходимого для инициации взрыва. Результатом оригинальной конструкции 1956 года было то, что более медленные нейтроны слишком сильно растягивали во времени реакцию и снижали общую мощность взрыва на выходе.
Этот эффект состоял в том, что сильно увеличивалось время между последующими событиями рождения нейтронов, которые необходимы для быстро нарастания взрыва, и это создает проблему в удержании условий для продолжения взрывного процесса; инерция, которая используется для удержания бомб имплозивного типа, не может удержать достаточно долго подобную реакцию по времени. Конечным результатом является взрыв с заметно более низкой урожайностью и с очень долгим временем горения вместо мощного ядерного взрыва. Прогнозируемый выход энергии будет порядка 1 т или 1000 т в тротиловом эквиваленте до 5 тысяч тонн эквивалента, вместо стандартного 20-килотонного взрывного выходя для того же количества используемого делящегося материала.
В классическом ядерном оружии критическая масса должна более или менее мгновенно породить взрывной процесс. Однако, если половина критической массы, U235 или U239, подвергается делению замедленными (тепловыми) или приторможенными (промежуточному) нейтронами, процесс будет продолжаться до тех пор, пока альфа-усиление (коэффициент производства нейтронов) будет положительным. Это вовлекает в процесс достаточное количества атомов, хотя его все еще недостаточно для мощного взрыва; Всегда будет выделяться достаточно энергии, в виде гамма или тормозного излучения, и условия процесса быстро "исчезают", прежде чем все это по-настоящему сильно взорвется. Несгоревшее дейтериевое топливо можно затем выгореть в огненном шаре, когда уже производство нейтронов или коэфициент альфа начинает затухать. Это можно достигнуть путем еще большего снижения критической массы путем добавления смеси гидратов лития 6 и дейтерия в сборку перед ее сжатием. Конечный результат - это то, что раньше называлось "хлопок" ("пшик"). В результате, вместо 20-килотонного вы получите только 5-килотонный взрыв, но он будет идти гораздо более длительное время в виде горения плазменного огненного шара.
* * *
продолжение - читайте через переводчик.
И так. Кандидат номер один - гидридная бомба. Возможно?
Я могу насчитать минимум ТРИ идеи как сделать мини-ядерную бомбу.
Самая простая и древняя идея - гидридная бомба (о ней я тут однажды уже спорил).
Я нашел в англоязычном интернете статью, авторы которой думают так же.
Статья спорная. Поэтому я ее перевел не всю а только начало.

VT Proving Again that Nuclear Weapons Are Your Friend – Veterans Today | Military Foreign Affairs Policy Journal for Clandestine Services
first published September 4th, 2015 We are now at the fifth generation of nuclear weapons design which means that a number of different types of nuclear weapon exist and they differ substantially in effect from the weapons we are familiar with from all those 1950s newsreels of huge atomic blasts. // Дальше — www.veteranstoday.comпервая публикация - 4 сентября 2015
VT Ядерное образование: уран-гидридная бомба
Ян Гринхалх совместно Джеффом Смитом.
Сейчас мы находимся на стадии разработки пятого поколения ядерного оружия, что означает, что существует целый ряд различных типов ядерного оружия, и они существенно отличаются по эффективности от того оружия, с которым мы знакомы по всем этим киножурналам 1950-х годов об огромных атомных взрывах.
* * *
Современное ядерное оружие 5-го поколения часто имеет гораздо меньшую мощность, чем бомбы Хиросимы и Нагасаки, с выходом менее 1 килотонны (1000 тонн в тротиловом эквиваленте). У него также иная динамика взрыва - вместо одного мощного короткого взрыва у его может быть намного более длительное время горения, что производит визуальные эффекты, которые выглядят совсем по-другому.
Вот почему важно кое-что узнать об этих новых типах оружия и о том, как его взрывы будут выглядеть визуально, поскольку это позволит лучше идентифицировать ядерные инциденты в будущем; позволяя людям различать обычные взрыв на складе, битком набатом ракетным топлива от настоящего ядерного взрыва.
Микроядерный тест на маленьком трейлере, показывающий, насколько маломощными могут быть это 5-е поколение.
Не надо самих себя обманывать, мы вступили в опасную новую эпоху, когда использование этого нового передового ядерного оружия малой мощности станет все более распространенным явлением; поэтому нам всем необходимо больше информации об этом оружии, чтобы все труднее можно было скрытно использовать его для совершения террора.
* * *
Уран-гидридная бомба представляет собой вариант конструкции атомной бомбы, впервые предложенный еще в 1939 году. В ней используется дейтерий, изотоп водорода, в качестве замедлителя нейтронов в имплозивном оружии на основе U235. Здесь нейтронная цепная реакция представляет собой замедленный процесс ядерного деления по сравнению с процессом ядерного деления быстрыми нейтронами в обычном заряде.
Из-за использования более медленно движущихся нейтронов в цепном процессе, на итоговый выход взрывной мощности бомб охлаждение нейтронов оказывает отрицательно влияет, поскольку оно растягивает во времени процесс размножения нейтронов или снижает скорость производства альфа. Достоверно известно, что две уран-гидридные бомбы были испытаны еще в 1950-х годах, при испытательных взрывах Рут и Рэй (Ruth and Ray) в ходе операции Upshot-Knothole, в 1956 году. Испытания выдали мощность, сравнимую примерно с 200 тоннами тротила каждое. Тем не менее, в то время оба теста считались неэффективными. Так как тогда была тенденция создавать оружия с большим взрывом выходом и технология была отложена на более чем 20 лет.
В конструкции такого ядерного оружия на замедленном или медленном делении, дейтерий в форме гидрида урана (UH3) или гидрида плутония (PUH3) замедляет (притормаживает) нейтроны, тем самым увеличивая сечение деления нейтронов. В результате достигается гораздо меньшая критическая масса и, следовательно, более компактное оружие, в котором снижается количество U235 или плутония PU239, необходимого для инициации взрыва. Результатом оригинальной конструкции 1956 года было то, что более медленные нейтроны слишком сильно растягивали во времени реакцию и снижали общую мощность взрыва на выходе.
Этот эффект состоял в том, что сильно увеличивалось время между последующими событиями рождения нейтронов, которые необходимы для быстро нарастания взрыва, и это создает проблему в удержании условий для продолжения взрывного процесса; инерция, которая используется для удержания бомб имплозивного типа, не может удержать достаточно долго подобную реакцию по времени. Конечным результатом является взрыв с заметно более низкой урожайностью и с очень долгим временем горения вместо мощного ядерного взрыва. Прогнозируемый выход энергии будет порядка 1 т или 1000 т в тротиловом эквиваленте до 5 тысяч тонн эквивалента, вместо стандартного 20-килотонного взрывного выходя для того же количества используемого делящегося материала.
В классическом ядерном оружии критическая масса должна более или менее мгновенно породить взрывной процесс. Однако, если половина критической массы, U235 или U239, подвергается делению замедленными (тепловыми) или приторможенными (промежуточному) нейтронами, процесс будет продолжаться до тех пор, пока альфа-усиление (коэффициент производства нейтронов) будет положительным. Это вовлекает в процесс достаточное количества атомов, хотя его все еще недостаточно для мощного взрыва; Всегда будет выделяться достаточно энергии, в виде гамма или тормозного излучения, и условия процесса быстро "исчезают", прежде чем все это по-настоящему сильно взорвется. Несгоревшее дейтериевое топливо можно затем выгореть в огненном шаре, когда уже производство нейтронов или коэфициент альфа начинает затухать. Это можно достигнуть путем еще большего снижения критической массы путем добавления смеси гидратов лития 6 и дейтерия в сборку перед ее сжатием. Конечный результат - это то, что раньше называлось "хлопок" ("пшик"). В результате, вместо 20-килотонного вы получите только 5-килотонный взрыв, но он будет идти гораздо более длительное время в виде горения плазменного огненного шара.
* * *
продолжение - читайте через переводчик.
И так. Кандидат номер один - гидридная бомба. Возможно?

Давайте прикинем что нам может дать гидрид.
Гидрид урана имеет плотность примерно в два раза меньше чем металлический уран 11 г/см3 (вместо 19 г/см3). На одно ядро урана в нем три атома водорода (вернее дейтерия). Задача замедлитеря - ПРИТОРМОЗИТЬ нейтроны. Это по-идее должно заметно уменьшить критическую массу сборки и как следствие, количество распыленного, непрореагировавшено в малом боеприпасе ценного актиноида. Мы будем все считать от урана, так как уран и дешевле плутония и "экологически чище" (как бы кому кощунственно это не показалось).
За основу рассуждений берем две странички от Феоктистов Л. П. Из прошлого в будущее
Критический размер пропроционален свободному пробегу нейтрона в сборке:
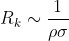
"ро" - плотность сборки, "сигма" - сечение взаимодействия (деления). Отсюда масса сборки - квадрат параметра:
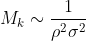 (1)
(1)
Критическая масса сферы из урана 235 имеет массу 52 кг.
Первый способ снизить эту массу - окружить ее отражателем. В "Лос-Аламасском букваре" показано что толстый отражатель теоретически снижает критическую массу в 4 раза.
Толстый отражатель из тяжелого материала хорошо заменяется более легким и тонким берилием, который имеет альбедо для нейтронов выше 1 (то есть возвращает нейтронов в критсборук больше чем на него упало).
То есть окружив берилием шар урана-235 вы можете уменьшить критическую массу до 13 кг.
Следующий шаг. Смотрим форумулу (1). Мы можем сжать материал. Как сказано у того же Феоктистова
для сжатия металла (на нашем уровне нет особой разницы какого) в 2 -2.5 раза нужно на 1 кг использовать 10 кг хорошей взрывчатки и качестввенная схема имплозии. Сжав нашу сборку в 2-2.5 раза мы уменьшим критическую массу еще в 4- 6,25 раз. То есть еще уменьшить массу критической сборки до 3,25-2 кг.
Реальный заряд должен быть в 3-4 раза больше (если мы не используем бустирование, то есть тритий).
То есть нормальная масса урана в нормальной чисто урановой сборке (обычно используют компазитный пит в центре плутоний - вокруг обогащенный уран) имеем 6-18 кг урана.
Это заряд номинальной мощности (с делением ~ 10% от заряженного и выходом 10-20 кт). По-сути все тонкие ущищнерия создателей зарядов сводятся уже к тому чтобы зарядить 6, а не 18 кг (опять же, бустирование мы тут не вспоминаем).
Если мы хотим получить взрыв малой мощности, в 0.1-0.01 кт, то нам не нужно 3-4-х кратного превышение критичности. Можно перейти критичность всего в 2 - 1.5 раза. То есть зарядить в пит маломощного заряда (типа ранцевой бомбы или Дэви Крокета) 6-3 кг. Ну а если вы такой заряд бустируете то вы получите номинальную мощность (20-40 кт).
Можно ли еще снизить критическую массу?
Можно сжимать еще сильней. Но это потребует заметного увеличения массы взрывчатки. Но в формуле (1) у нас есть еще один фактор - сигма - сечение взаимодейтсвия. Если его поднять, это существенно снизит критичесую массу. Например сигма плутония чуть больше сигры урана, и это приводит к тому что сфера из плутония имеет критичесую массу всего в 11 кг.
Мы знаем, что если замедлить нейтроны, то можно увеличить сечение взаимодействие. Но проблема в том, что взаимодействие не огнаничивается делением. Есть сечение рассеения (только в одном из черырех столкновений нейтрон делит, а в трех - упруго отскакивает), есть сечение неупругого рассеивания, есть сечение поглащения (и ядро 235 вместо того что бы распастья испускае гамму и начинет трансмутировать). Поэтому так просто сказать будет ли толк от некоторого замедления нейтронов - сложно.
Мои потуги "на салфетке".
Если верить этому графику, то есть смысл замедлять нейтроны только в 100 раз (до примерно 10 кэВ) и это позволяет поднять сечение деления урана примерно в 3.5 раза. То есть, критическая масса снижается еще более чем в 12 раз! (при прочем равном, в частности плотности урана, а в гидриде она ниже).
Но по графику видно, что помимо сечения деления быстро растет и сечение захвата (выделено темно-синим) не только 238 но даже 235-го! Еще немного торможения и захват становится более вероятным чем деление (область возможного для бомбы я выделил желтым) и так продолжается до энергий нейтронов в электронвольты, что выделено синим (область реакторных цепных процессов).
В общем, гидридная бомба, если и может работать, то она работает "на краю". Требует очень точной настройки всей конструкции. Но интересно все же прикинуть возможности. Если мы допустим, что гидрид сжиматся примерно так же как и обычный уран, то при сжатии того в 2.7 раза с хорошим бериллиевым отражателем (толщиной не меньше радиуса сжатой сборки) то можно рассчитывать на критическую массу в ... 660 грамм ВОУ.
При этом, возможно, нам и не нужен ВОУ. Влияние 238-го тут может оказаться незначительным (второй тест 1956-го выдал те же 200 т ТНТ что и первый, хотя в нем заряжался уран куда меньшего обогащения).
Моя гипотеза на рисунке отмечена темно-синим и красным столбиком. Видно что сечение захвата в нашей рабочей области у 235-го растет быстрей чем у 238-го, поэтому наличие 238-го не сильно и влияет на динамику процесса.
Если мы зарядим в гидридную бомбу три критических массы (то есть хотим получить максимальный выход в примерно 200 т ТНТ) то нам нужен шарик гидрида в 7 см диаметром и массой почти 2 кг.
Гидрид урана имеет плотность примерно в два раза меньше чем металлический уран 11 г/см3 (вместо 19 г/см3). На одно ядро урана в нем три атома водорода (вернее дейтерия). Задача замедлитеря - ПРИТОРМОЗИТЬ нейтроны. Это по-идее должно заметно уменьшить критическую массу сборки и как следствие, количество распыленного, непрореагировавшено в малом боеприпасе ценного актиноида. Мы будем все считать от урана, так как уран и дешевле плутония и "экологически чище" (как бы кому кощунственно это не показалось).
За основу рассуждений берем две странички от Феоктистов Л. П. Из прошлого в будущее
Критический размер пропроционален свободному пробегу нейтрона в сборке:
"ро" - плотность сборки, "сигма" - сечение взаимодействия (деления). Отсюда масса сборки - квадрат параметра:
Критическая масса сферы из урана 235 имеет массу 52 кг.
Первый способ снизить эту массу - окружить ее отражателем. В "Лос-Аламасском букваре" показано что толстый отражатель теоретически снижает критическую массу в 4 раза.
Толстый отражатель из тяжелого материала хорошо заменяется более легким и тонким берилием, который имеет альбедо для нейтронов выше 1 (то есть возвращает нейтронов в критсборук больше чем на него упало).
То есть окружив берилием шар урана-235 вы можете уменьшить критическую массу до 13 кг.
Следующий шаг. Смотрим форумулу (1). Мы можем сжать материал. Как сказано у того же Феоктистова
для сжатия металла (на нашем уровне нет особой разницы какого) в 2 -2.5 раза нужно на 1 кг использовать 10 кг хорошей взрывчатки и качестввенная схема имплозии. Сжав нашу сборку в 2-2.5 раза мы уменьшим критическую массу еще в 4- 6,25 раз. То есть еще уменьшить массу критической сборки до 3,25-2 кг.
Реальный заряд должен быть в 3-4 раза больше (если мы не используем бустирование, то есть тритий).
То есть нормальная масса урана в нормальной чисто урановой сборке (обычно используют компазитный пит в центре плутоний - вокруг обогащенный уран) имеем 6-18 кг урана.
Это заряд номинальной мощности (с делением ~ 10% от заряженного и выходом 10-20 кт). По-сути все тонкие ущищнерия создателей зарядов сводятся уже к тому чтобы зарядить 6, а не 18 кг (опять же, бустирование мы тут не вспоминаем).
Если мы хотим получить взрыв малой мощности, в 0.1-0.01 кт, то нам не нужно 3-4-х кратного превышение критичности. Можно перейти критичность всего в 2 - 1.5 раза. То есть зарядить в пит маломощного заряда (типа ранцевой бомбы или Дэви Крокета) 6-3 кг. Ну а если вы такой заряд бустируете то вы получите номинальную мощность (20-40 кт).
Можно ли еще снизить критическую массу?
Можно сжимать еще сильней. Но это потребует заметного увеличения массы взрывчатки. Но в формуле (1) у нас есть еще один фактор - сигма - сечение взаимодейтсвия. Если его поднять, это существенно снизит критичесую массу. Например сигма плутония чуть больше сигры урана, и это приводит к тому что сфера из плутония имеет критичесую массу всего в 11 кг.
Мы знаем, что если замедлить нейтроны, то можно увеличить сечение взаимодействие. Но проблема в том, что взаимодействие не огнаничивается делением. Есть сечение рассеения (только в одном из черырех столкновений нейтрон делит, а в трех - упруго отскакивает), есть сечение неупругого рассеивания, есть сечение поглащения (и ядро 235 вместо того что бы распастья испускае гамму и начинет трансмутировать). Поэтому так просто сказать будет ли толк от некоторого замедления нейтронов - сложно.
Мои потуги "на салфетке".
Если верить этому графику, то есть смысл замедлять нейтроны только в 100 раз (до примерно 10 кэВ) и это позволяет поднять сечение деления урана примерно в 3.5 раза. То есть, критическая масса снижается еще более чем в 12 раз! (при прочем равном, в частности плотности урана, а в гидриде она ниже).
Но по графику видно, что помимо сечения деления быстро растет и сечение захвата (выделено темно-синим) не только 238 но даже 235-го! Еще немного торможения и захват становится более вероятным чем деление (область возможного для бомбы я выделил желтым) и так продолжается до энергий нейтронов в электронвольты, что выделено синим (область реакторных цепных процессов).
В общем, гидридная бомба, если и может работать, то она работает "на краю". Требует очень точной настройки всей конструкции. Но интересно все же прикинуть возможности. Если мы допустим, что гидрид сжиматся примерно так же как и обычный уран, то при сжатии того в 2.7 раза с хорошим бериллиевым отражателем (толщиной не меньше радиуса сжатой сборки) то можно рассчитывать на критическую массу в ... 660 грамм ВОУ.
При этом, возможно, нам и не нужен ВОУ. Влияние 238-го тут может оказаться незначительным (второй тест 1956-го выдал те же 200 т ТНТ что и первый, хотя в нем заряжался уран куда меньшего обогащения).
Моя гипотеза на рисунке отмечена темно-синим и красным столбиком. Видно что сечение захвата в нашей рабочей области у 235-го растет быстрей чем у 238-го, поэтому наличие 238-го не сильно и влияет на динамику процесса.
Если мы зарядим в гидридную бомбу три критических массы (то есть хотим получить максимальный выход в примерно 200 т ТНТ) то нам нужен шарик гидрида в 7 см диаметром и массой почти 2 кг.
Прикреплённые файлы:

Это сообщение редактировалось 10.10.2019 в 13:05
Конечно, наша битва за снижение критической массы для урана (плутоний мы вообще не рассматриваем пока) за счет притормаживания нейтронов не может быть безнаказанной.
Во-первых у нас растягивается "тау" - время удвоения поколений. И это главная причина, почему такая бомба не может выдать нам полноценные килотонны. Если мы уменьшили энергию нейтронов в 100 раз, это означает что скорость нейтронов упала в 10 раз. И значит интервал между поколениями так же растянулся в 10 раз. А это показатель в экспоненте же! Хотя, не все так плохо.
Мы же ведь используем имплозию. А это значит что мы уменьшаем расстояние между атомами урана в корень из сжатия. 2.7 раза сжали, расстояние уменьшилось в 1.6 раз. Значит и сжали тау. Не бог весть во сколько. Но учитывая что у нас цепной процесс (экспонента) то эффект от такого сжатия на общее количество нейтронов получается ехр(1.6) ~ 5 раз.
Не зря в пушечной схеме мы можем получить лишь ~ 1 % выгорания, а при сжатии всего в 2-2.5 раза при имплозии уже более 10%.
В гидридной бомбе имплозия так же является, видимо, единственной подпоркой, ускоряющей цепной процесс (и только имплозивная гидридная бомба может взорваться).
Все остальное работает на его тушение. Например, если у вас слишком много замедлителя, у вас нейтроны начнут слишком быстро тормозить.
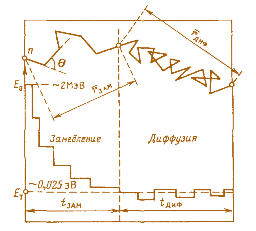
Хитрость в том, что бы в сборке, в среднем, каждый нейтрон прошел не более 4-5 столкновений с замедлителем иначе он замедлится слишком сильно, а это - его потеря для процесса взрыва. Да, до тепловых нейтронов ему будет еще далеко (18 столкновений) но сильно замедлившись он как бы "исчезнет" из цепного процесса. Он будет в сборке, но он будет "в пути". Это можно было бы ввести в расчет критичности как своего рода дополнительно "поглощение" нейтронов.
В общем. Тут масса нюансов. Нужно, видимо, хорошее моделирование. А учитывая гидродинамику, все становится совсем туманным. Сборка ведь себя ведет как жидкость и в сущности при сжатии она никогда не имеет одинаковую плотность, в каком то месте она сжата сильно (на фронте ударной волны), в каком то месте слабо (далеко за фронтом)...
...точный расчет подобного устройства становится задачей для совсем умных...
Ударная волна сжатия сначала движется в центр пита, потом отражается...
В общем, все очень сложно.
Не зря птенцы Эдварда Тэллера в новой бомбовой лаборатории полезли эксперементировать и их эксперимент не совпал с рачетами (видимо их расчетные модели даже в 1956-м были слишком грубыми и чересчур оптимистичными).
Однако. Я все же рискну предположить, что можно выжать таки 200 тонн ТНТ из 2 кг гидрида урана (3 критических массы) использовав для сжатия 20 кг октогена. И я решил прикинуть как это будет выглядеть. Нарисовал все в масштабе 1 к 1 (что бы "пощупать" глазами конструкцию). У меня получилось вот что
Нажмите в просмотрщике "реальный масштаб". Тогда вы ощутит реальные габариты.
Это конечно художество. При этом я показал монолоитный пит (что глупость, надо в центре оставить половину массы, а остальную - раскатать в полую сферу вплотную к бериллию). Взрывная линза здесь - "Лебедь". В итоге батон получился очень даже крупным... 30 см в диаметре и массой под 50 кг.
Это, я думаю, предел портативности для подобного изделия.
Главный тут вопрос -цена. Пусть я перестраховался с 3 критмассами. Допустим хватит 2-х или даже 1.5. Это позволит использовать в пите не 90% ВОУ а всего 75 или даже 50% обогащения. Такой уран много дешевле (если гидридная бомба не чувствительна к степени обогащения, а это возможно ее конек). Тогда подобных "батонов" можно было бы налепить достаточно много и достаточно массово их применять на поле боя.
Я под это дело даже придумал АИ (альтернативную историю). Мол, война с немцами затянулась до 1947-го и боши таки схватились за задницу в 1945-м (там вообще было перемирие с 1944-го до 1946-го) и начали делать бомбу. И вот тогда сумрачный германский гений начал бы делать не супербомбу для одного большого фейерверка (не серьезно это), а запустил бы производство вот таких вот более дешевых и массовых гидридных девайсов под малую мощность (ведь эффективность в зоне разрушения падает с корнем кубическим от мощности!) и начал бы засыпать противника на фронтах с блицбомберов десятками гидридных атомных бомб, полагая что лучше сорок раз по разу чем ни разу сорок раз. Даже начал наклевываться сюжет для статической кампании в "Ил-2 1946" (ведь внешне взрыв в 100 тонн тнт мало отличается от взрыва в 5-8 т тнт, который можно организовать в редакторе миссий засыпав карту ударами внезапно появляющихся прямо у цели "мистралей" и организовать под крылом игрока настоящий "ад и Израиль". Игрок у нас конечно всего лишь наружный наблюдатель. Он у нас истребитель на Ta-183).
(ведь внешне взрыв в 100 тонн тнт мало отличается от взрыва в 5-8 т тнт, который можно организовать в редакторе миссий засыпав карту ударами внезапно появляющихся прямо у цели "мистралей" и организовать под крылом игрока настоящий "ад и Израиль". Игрок у нас конечно всего лишь наружный наблюдатель. Он у нас истребитель на Ta-183).
Во-первых у нас растягивается "тау" - время удвоения поколений. И это главная причина, почему такая бомба не может выдать нам полноценные килотонны. Если мы уменьшили энергию нейтронов в 100 раз, это означает что скорость нейтронов упала в 10 раз. И значит интервал между поколениями так же растянулся в 10 раз. А это показатель в экспоненте же! Хотя, не все так плохо.
Мы же ведь используем имплозию. А это значит что мы уменьшаем расстояние между атомами урана в корень из сжатия. 2.7 раза сжали, расстояние уменьшилось в 1.6 раз. Значит и сжали тау. Не бог весть во сколько. Но учитывая что у нас цепной процесс (экспонента) то эффект от такого сжатия на общее количество нейтронов получается ехр(1.6) ~ 5 раз.
Не зря в пушечной схеме мы можем получить лишь ~ 1 % выгорания, а при сжатии всего в 2-2.5 раза при имплозии уже более 10%.
В гидридной бомбе имплозия так же является, видимо, единственной подпоркой, ускоряющей цепной процесс (и только имплозивная гидридная бомба может взорваться).
Все остальное работает на его тушение. Например, если у вас слишком много замедлителя, у вас нейтроны начнут слишком быстро тормозить.

Хитрость в том, что бы в сборке, в среднем, каждый нейтрон прошел не более 4-5 столкновений с замедлителем иначе он замедлится слишком сильно, а это - его потеря для процесса взрыва. Да, до тепловых нейтронов ему будет еще далеко (18 столкновений) но сильно замедлившись он как бы "исчезнет" из цепного процесса. Он будет в сборке, но он будет "в пути". Это можно было бы ввести в расчет критичности как своего рода дополнительно "поглощение" нейтронов.
В общем. Тут масса нюансов. Нужно, видимо, хорошее моделирование. А учитывая гидродинамику, все становится совсем туманным. Сборка ведь себя ведет как жидкость и в сущности при сжатии она никогда не имеет одинаковую плотность, в каком то месте она сжата сильно (на фронте ударной волны), в каком то месте слабо (далеко за фронтом)...
...точный расчет подобного устройства становится задачей для совсем умных...
Ударная волна сжатия сначала движется в центр пита, потом отражается...
В общем, все очень сложно.
Не зря птенцы Эдварда Тэллера в новой бомбовой лаборатории полезли эксперементировать и их эксперимент не совпал с рачетами (видимо их расчетные модели даже в 1956-м были слишком грубыми и чересчур оптимистичными).
Однако. Я все же рискну предположить, что можно выжать таки 200 тонн ТНТ из 2 кг гидрида урана (3 критических массы) использовав для сжатия 20 кг октогена. И я решил прикинуть как это будет выглядеть. Нарисовал все в масштабе 1 к 1 (что бы "пощупать" глазами конструкцию). У меня получилось вот что
Нажмите в просмотрщике "реальный масштаб". Тогда вы ощутит реальные габариты.
Это конечно художество. При этом я показал монолоитный пит (что глупость, надо в центре оставить половину массы, а остальную - раскатать в полую сферу вплотную к бериллию). Взрывная линза здесь - "Лебедь". В итоге батон получился очень даже крупным... 30 см в диаметре и массой под 50 кг.
Это, я думаю, предел портативности для подобного изделия.
Главный тут вопрос -цена. Пусть я перестраховался с 3 критмассами. Допустим хватит 2-х или даже 1.5. Это позволит использовать в пите не 90% ВОУ а всего 75 или даже 50% обогащения. Такой уран много дешевле (если гидридная бомба не чувствительна к степени обогащения, а это возможно ее конек). Тогда подобных "батонов" можно было бы налепить достаточно много и достаточно массово их применять на поле боя.
Я под это дело даже придумал АИ (альтернативную историю). Мол, война с немцами затянулась до 1947-го и боши таки схватились за задницу в 1945-м (там вообще было перемирие с 1944-го до 1946-го) и начали делать бомбу. И вот тогда сумрачный германский гений начал бы делать не супербомбу для одного большого фейерверка (не серьезно это), а запустил бы производство вот таких вот более дешевых и массовых гидридных девайсов под малую мощность (ведь эффективность в зоне разрушения падает с корнем кубическим от мощности!) и начал бы засыпать противника на фронтах с блицбомберов десятками гидридных атомных бомб, полагая что лучше сорок раз по разу чем ни разу сорок раз. Даже начал наклевываться сюжет для статической кампании в "Ил-2 1946"
 (ведь внешне взрыв в 100 тонн тнт мало отличается от взрыва в 5-8 т тнт, который можно организовать в редакторе миссий засыпав карту ударами внезапно появляющихся прямо у цели "мистралей" и организовать под крылом игрока настоящий "ад и Израиль". Игрок у нас конечно всего лишь наружный наблюдатель. Он у нас истребитель на Ta-183).
(ведь внешне взрыв в 100 тонн тнт мало отличается от взрыва в 5-8 т тнт, который можно организовать в редакторе миссий засыпав карту ударами внезапно появляющихся прямо у цели "мистралей" и организовать под крылом игрока настоящий "ад и Израиль". Игрок у нас конечно всего лишь наружный наблюдатель. Он у нас истребитель на Ta-183).
Прикреплённые файлы:
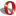

Это сообщение редактировалось 09.10.2019 в 21:47
Гидридная бомба - это только один вариант нового поколения ЯО (первый вариант, но не последний). Пятого, четвертого поколения (или второго-бис) - не суть важно.
Товарищи в статье выше, как мне кажется "гонят беса", уверяя что подобное оружие уже давно используется (они там прям кучу фоток приводят).
Занимательно и то, что авторы статьи уверены, что раз гидридная бомба ТЕОРЕТИЧЕСКИ "горит" медленней, то и эффект ее взрыва окажется иным, не таким как у "обычной" атомной (водородной) бомбы.
Но я думаю что это глупость.
Разница между 8 и 7-ю порядками "на глаз" неотличима и поэтому гидридная бомба будет взрываться так же как и обычная. Вспышка, ударная волна. Никакого "медленного горения"....
Ну и радиоактивный фон. Как не верти, но будет наведенная радиация и будет выпадение высокоактивных продуктов деления. При этом так как подобный взрыв, в основном "наземный" (близко к поверхности или на самой поверхности) выпадение тех граммов продуктов деления будет хоть и очень локальным (гриб высоко не поднимается и далеко не уносит "перегар"), но очень плотным (и поэтому в очень малом месте будет очень сильное заражение первые сутки). Плюс наведенная вспышкой нейтроном радиация тоже будет не хилой первое время. Не думаю, что применение подобных устройств можно реально долго скрывать. Были бы явно пострадавшие от лучевой болезни.
Хотя... В нашем сумасшедшем мире... "Есть много друг Гораций такого, ...."
Еще. Если концепция столь старая (по сути еще с 1943-го года рождения. Не зря там в статье в недопереведенной мной части приводятся и слова Опенгеймера о гидриде для бомбы) то что тут нового?
Новое - чудовищное падение цены на ВОУ за счет доведения технологии центрифугирования до предела совершенства. Новое что нарезая по 2 кг обогащенного до 50% урана, какой-нибудь Пакистан может себе позволить наделать тысячи и тысячи "обычных" боеприпасов повышенной мощности (или Великая Корея перестанет догонять и начнет лидировать?) для массового применения именно на поле боя. Себестоимость ВОУ за пол века упала в цене на несколько порядков (надо поднять данные насколько точно). Центрифуги творят чудеса. При этом рыночная цена - не показатель (его цена - как цена золота, скорей предмет даже политических, а не экономических спекуляций, хотя правда видимо в комбинации и того и другого).
Товарищи в статье выше, как мне кажется "гонят беса", уверяя что подобное оружие уже давно используется (они там прям кучу фоток приводят).
Занимательно и то, что авторы статьи уверены, что раз гидридная бомба ТЕОРЕТИЧЕСКИ "горит" медленней, то и эффект ее взрыва окажется иным, не таким как у "обычной" атомной (водородной) бомбы.
Но я думаю что это глупость.
Разница между 8 и 7-ю порядками "на глаз" неотличима и поэтому гидридная бомба будет взрываться так же как и обычная. Вспышка, ударная волна. Никакого "медленного горения"....
Ну и радиоактивный фон. Как не верти, но будет наведенная радиация и будет выпадение высокоактивных продуктов деления. При этом так как подобный взрыв, в основном "наземный" (близко к поверхности или на самой поверхности) выпадение тех граммов продуктов деления будет хоть и очень локальным (гриб высоко не поднимается и далеко не уносит "перегар"), но очень плотным (и поэтому в очень малом месте будет очень сильное заражение первые сутки). Плюс наведенная вспышкой нейтроном радиация тоже будет не хилой первое время. Не думаю, что применение подобных устройств можно реально долго скрывать. Были бы явно пострадавшие от лучевой болезни.
Хотя... В нашем сумасшедшем мире... "Есть много друг Гораций такого, ...."
Еще. Если концепция столь старая (по сути еще с 1943-го года рождения. Не зря там в статье в недопереведенной мной части приводятся и слова Опенгеймера о гидриде для бомбы) то что тут нового?
Новое - чудовищное падение цены на ВОУ за счет доведения технологии центрифугирования до предела совершенства. Новое что нарезая по 2 кг обогащенного до 50% урана, какой-нибудь Пакистан может себе позволить наделать тысячи и тысячи "обычных" боеприпасов повышенной мощности (или Великая Корея перестанет догонять и начнет лидировать?) для массового применения именно на поле боя. Себестоимость ВОУ за пол века упала в цене на несколько порядков (надо поднять данные насколько точно). Центрифуги творят чудеса. При этом рыночная цена - не показатель (его цена - как цена золота, скорей предмет даже политических, а не экономических спекуляций, хотя правда видимо в комбинации и того и другого).

Это сообщение редактировалось 09.10.2019 в 21:55
A.s.> Господи, этот то тут причем? Для Украины (не говоря уже о Зеленском) ЯО 4-го поколения это еще "круче" чем гиперлуп или база на Луне!!!
Ну почему сразу 4 поколение? Открою тайну. Здесь еще в 2014 году обсуждали может ли Украина получить ЯО. Решили что сможет. Только для этого нужна очень большая сила воли у руководства. И получить она сможет только несколько штук. Так как после первого же испытания прекратятся поставки урана для АЭС и разных химикатов.
Ну почему сразу 4 поколение? Открою тайну. Здесь еще в 2014 году обсуждали может ли Украина получить ЯО. Решили что сможет. Только для этого нужна очень большая сила воли у руководства. И получить она сможет только несколько штук. Так как после первого же испытания прекратятся поставки урана для АЭС и разных химикатов.

Copyright © Balancer 1997..2025
Создано 07.10.2019
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
Создано 07.10.2019
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
 Alex_semenov
Alex_semenov

 инфо
инфо инструменты
инструменты Oleg_NZH
Oleg_NZH


 Xan
Xan

 Naib
Naib









